Overview and Objective
In this lesson, students explore the properties of Taxicab geometry. They discover the effects of the changing distance definition on geometrical shapes while creating taxicab circles and ellipses.
Warm-Up
Taxicab geometry is a form of geometry in which you can only move along the lines of a grid, rather than along diagonal lines in the grid. Taxicab geometry uses the same points, lines, and angles as in Euclidean geometry. However, the distance between two points is calculated differently.
Use this Polypad to demonstrate the difference between the Euclidean and the taxicab geometry.
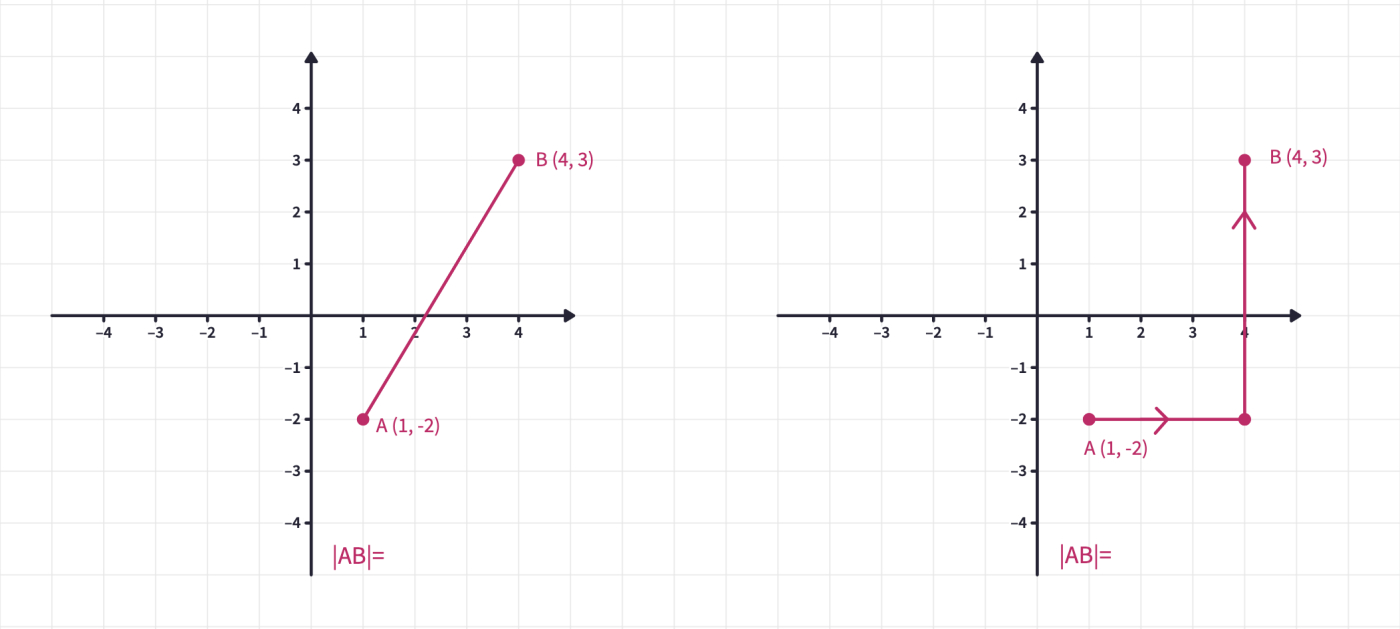
Ask students to determine the distance between points A and B in Euclidian geometry and in taxicab geometry. If students are already familiar with the Euclidian distance formula, ask them to come up with a formula for taxicab geometry too.
Allow students time to work on different points to find a general formula for the Taxicab distance.
For any two points on the coordinate plane such as and
In Euclidian geometry
and
in Taxicab geometry
Main Activity
Start by asking students the definition of circles.
A circle is the set of all points in two dimensions, at a fixed distance (the radius) from a given point (the center).
Remind them that the Taxicab geometry changes the notion of distance. Invite them to draw a Taxicab circle with a radius of 4 units.
You may also consider playing the game Catch me if you can by grouping students in pairs and letting them discover and play with the Taxicab circles concept.
In the second part of the lesson, ask students to predict the shape of taxicab ellipses. You may also remind them about the definition of an ellipse to help them make their predictions.
An ellipse is a curved path that surrounds two focal points. Any point on the circumference of the ellipse has the same sum of distances to the two foci.
Share this Polypad with students and ask them to complete the taxicab ellipse.
Before they start making their drawings, ask the total taxicab distance of each given point to focal points and .
Clarify with the students that points C, D, E, and F are the points on the circumference taxicab ellipse. They all have units as the sum of distances to the two foci.
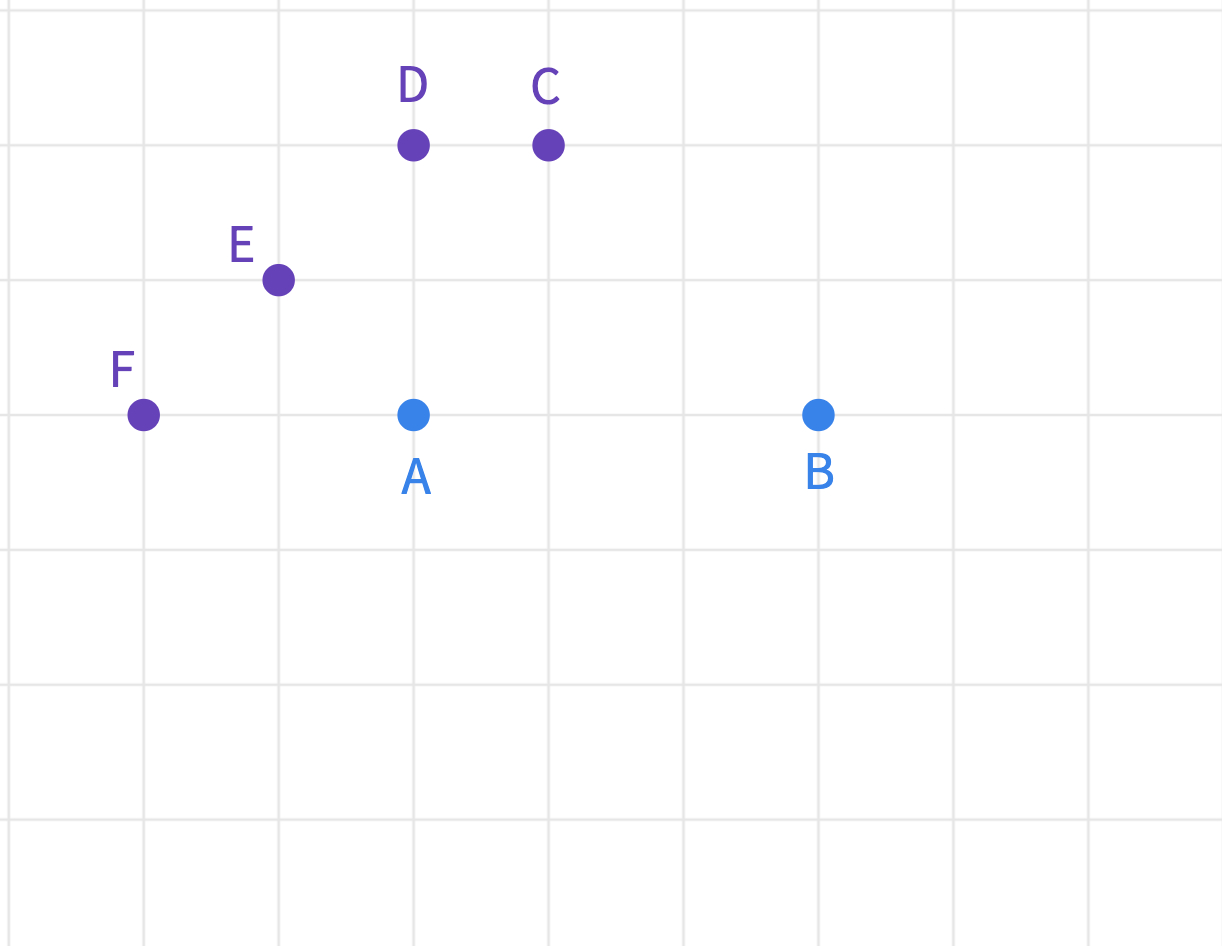
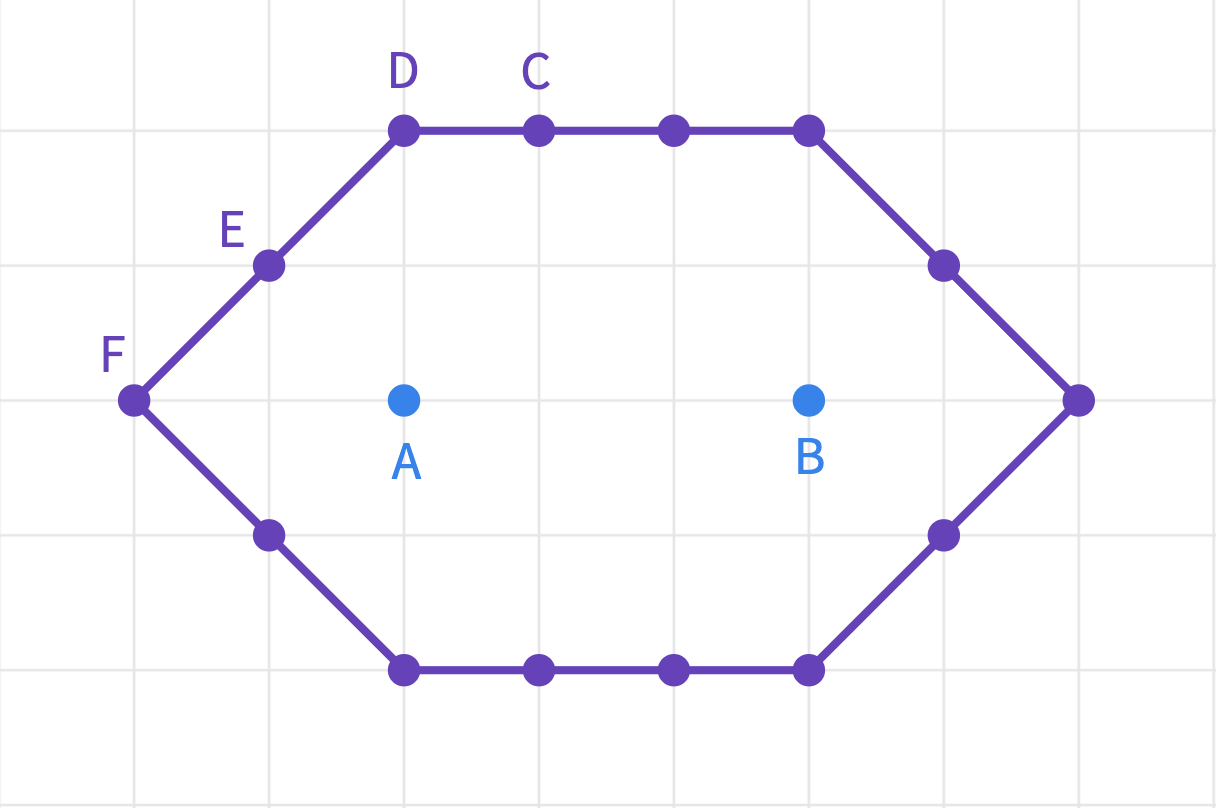
Consider having students work on this in groups to try different distances. Another group can work on the focal points of A and B that are only 2 units apart or in a different orientation. Let each group have a different A, B pair to work on.
Closure
Invite each group to share their work with the class. Here are possible drawings;
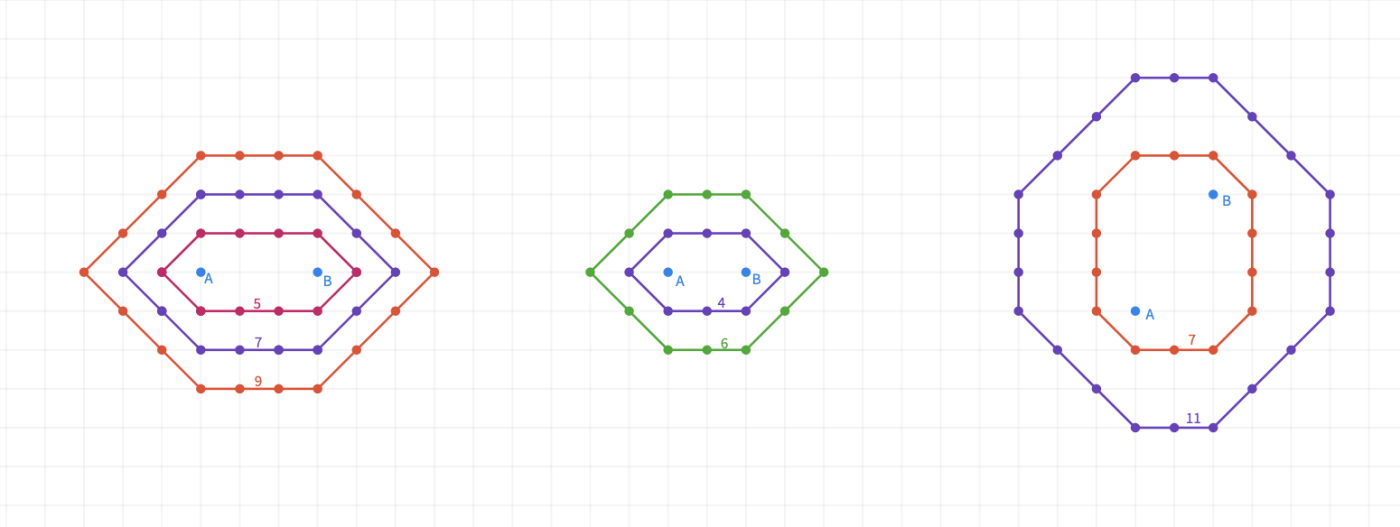
Clarify with the students that the taxicab ellipses are usually polygons like hexagons and octagons.
If students did not already reach a conclusion about rectangles before, as an exit ticket, you may want students to investigate if a rectangle (and a square) can be formed as a taxicab ellipse.
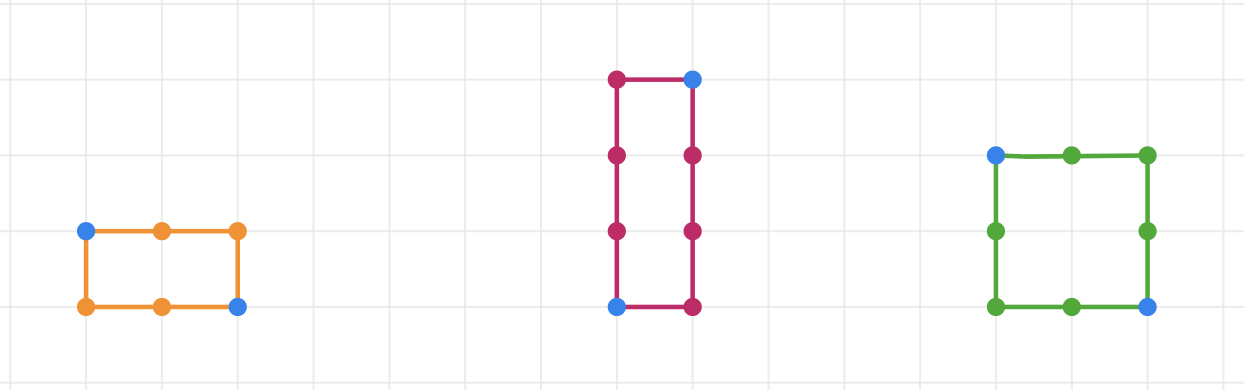
Let them share their findings and clarify that if the focal points are also on the circumference of the ellipse, rectangles can be formed as taxicab ellipses.
Support and Extension
For students ready for additional extension in this lesson, consider asking questions
In Euclidian geometry, If the foci are very close, the ellipse looks almost like a circle. As they move further apart, the ellipse becomes more elongated. Discuss with students how Taxicab ellipses are affected by the distance and the orientation of the focal points.

Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account.
Click here to learn how to share Polypads with students and how to view their work.