Divizibilitate și Numere PrimeDistribuția Numerelor Prime
Cea mai simpla metodă de a verifica dacă un număr este prim este să încerci sa-l împarți la toate numerele întregi mai mici decât el. Calculatoarele pot face asta foarte rapid și eficient. Pentru numere foarte mari, cu sute de cifre, există algoritmi mai eficienți. Unii dintre aceștia folosesc chiar și probabilități pentru a determina dacă un număr este aproape sigur prim.
Iată un calculator care îți permite să verifici daca un număr oarecare e prim:
Verificator de Numere Prime
Oamenii au încercat de-a lungul timpului să găsească numere prime din ce în ce mai mari. În anul 1460, cel mai mare număr prim cunoscut era 131.071. În 1772,
O dată cu sosirea calculatoarelor în secolul 20, calcularea numerelor prime mari a devenit mult mai ușoară. Cel mai mare număr prim cunoscut la ora actuală a fost descoperit în decembrie 2018 și are 24.862.048 cifre. Am avea nevoie de 8000 de foi de hârtie pentru a-l tipări!

GIMPS (Great Internet Mersenne Prime Search) este un proiect colaborativ în care volunarii pot găsi numere prime folosind software gratuit.
Calculul acestor numere prime mari ar putea părea a fi doar o pierdere de timp, dar mai târziu vei învăța în acest curs despre variatele aplicatii din viața reală în care calculatoarele au nevoie să folosească numere prime mari.
Aici poți genera propriile tale numere prime cu un număr dat de cifre:
Generator de Numere Prime
Numar cifre:
Spirala Ulam
Matematicianul polonez
Notăm toate numerele întregi într-o grilă dreptunghiulară, începând cu 1 în mijloc și apoi mergând în spirală spre exterior. Apoi subliniem toate numerele prime.
Momentan, spirala Ulam nu pare deosebit de interesantă. Dar, dacă o mărim, apar modele interesante. Iată numerele prime până la 160.000:
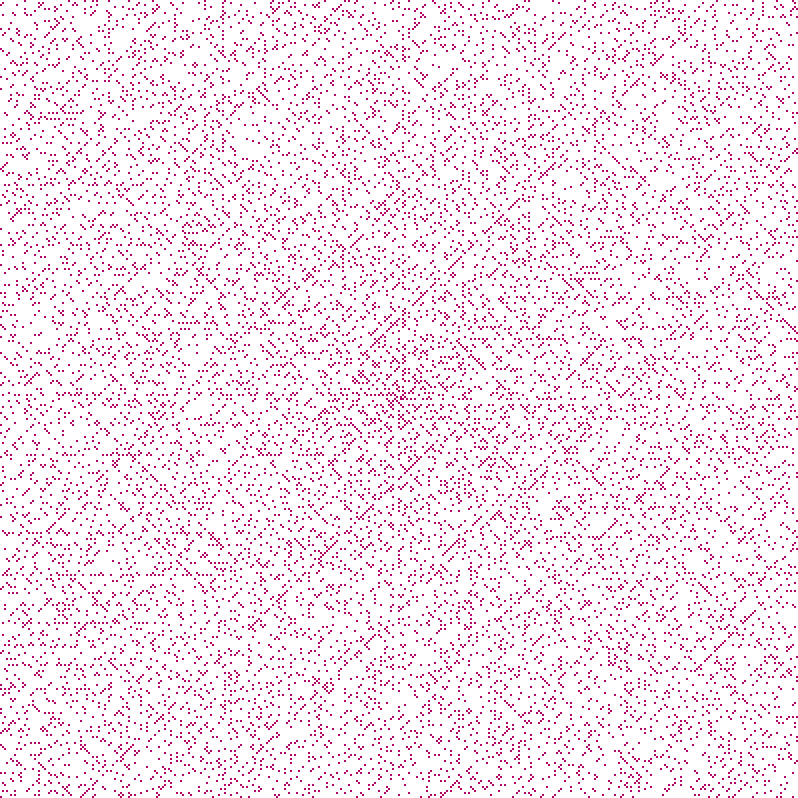
În loc să apară în mod aleator, așa cum ne-am putea aștepta, pare că anumite diagonale conțin mai multe numere prime ca altele. Se crează astfel un model "în carouri" interesant.
Se dovedește că toate aceste diagonale corespund anumitor ecuații de gradul al doilea care par să genereze numere prime mai des decât media. Cu toate acestea nu se știe de ce se întâmplă așa.
Coperta revistei Scientific American din Martie 1964
Conjectura lui Goldbach
În anul 1742, matematicianul german
Calculatorul Goldbach
Alege un număr par oarecare pentru a calcula cum
se poate scrie ca sumă a două numere prime.
Goldbach a scris despre constatarea sa într-o scrisoare adresată faimosului matematician
Calculatoarele au verificat că această Conjectură a lui Goldbach funcționează pentru orice număr par până la 4 × 1018 (un 4 urmat de 18 zerouri), dar matematicienii nu au demonstrat încă faptul că ea functionează pentru toate numerele întregi pare. Si asta constituie o diferență mare pentru că există o infinitate de numere întregi, așa că nu am avea cum să le verificăm pe toate.
Simplitatea aparentă a acestei conjecturi a făcut ca ea să fie una din cele mai faimoase probleme nerezolvate din matematică.
Numere Prime Gemene
Am văzut deja că numerele prime se distanțeaza tot mai mult pe măsură ce devin mai mari. Dar ele par să apară mereu complet aleator și ocazional găsim două numere prime alăturate, la doar un număr distanță: acestea se numesc Numere Prime Gemene.
35,1113,4143,101103,20272029,108,377108,379,1,523,6511,523,653
Cea mai mare pereche cunoscută de numere prime are 58.711 cifre! Dar există oare o infinitate de numere prime gemene, așa cum există o infinitate de numere prime? Nu se știe – Conjectura Numerelor Prime Gemene este o altă problemă nerezolvată cu privire la numerele prime.
Ipoteza Riemann
Matematicienii au explorat timp de multe secole modelul și distribuția numerelor prime. Acestea par să apară complet aleator - uneori există spații mari între numerele prime consecutive, iar alteori găsim
Pe când avea doar 15 ani, matematicianul german
De-a lungul axei X se pot vedea toate numerele întregi. La fiecare număr prim Funcția de Numărare a Numerelor Prime (marcată cu albastru) crește cu 1. Pe măsură ce
Cu toate acestea, după cum am văzut mai sus, încă există o abatere semnificativă între numărul actual de numere prime și aproximarea lui Gauss. În 1859, matematicianul
Sute de matematicieni au incercat să demonstreze ipoteza lui Riemann, dar toate încercările au fost fără succes. Este adesea considerată una din cele mai dificile și importante probleme nerezolvate din matematică. În anul 2000, Institutul de Matematică Clay a numit-o una din cele șapte