fractaliiIntroducere
Când priviți în jurul naturii, este posibil să fi observat plante complicate ca acestea:


Acest brad este format din multe frunze mici care se ramifică de una mai mare.


Acest broccoli Romanesco este format din
Inițial, acestea apar ca niște forme extrem de complexe - dar atunci când te uiți mai atent, ai putea observa că ambele respectă un model relativ simplu: toate părțile individuale ale plantelor arată exact la fel ca întreaga plantă, doar mai mici. Același tipar se repetă din nou, la scări mai mici.
În matematică, numim această proprietate auto-asemănare , iar formele care o au se numesc
Pentru a ne crea propriile fractale, trebuie să începem cu un model simplu și apoi să îl repetăm iar și iar, la scări mai mici.
Unul dintre cele mai simple modele ar putea fi un segment de linie , cu încă două segmente care se ramifică dintr-un capăt. Dacă repetăm acest tipar, ambele segmente albastre vor avea și alte două ramuri la capetele lor.
Puteți muta punctele albastre pentru a schimba lungimea și unghiul tuturor ramurilor. Apoi măriți numărul de iterații folosind
În funcție de poziția ramurilor, puteți face tipare complet diferite - arătând ca deasupra, un sau . Ce mai găsești?
Un alt fractal celebru este
Observați cum forma finală este alcătuită din trei copii identice ale sale , și fiecare dintre acestea este alcătuită din copii chiar mai mici ale întregului triunghi! Puteți continua să faceți zoom-ul în triunghi pentru totdeauna, iar modelele și formele vor continua să se repete.
Plantele de la începutul acestui capitol arată la fel ca fractalele, dar este clar imposibil să creezi fractali adevărați în viața reală. Dacă continuăm să repetăm același model de mai multe ori, din ce în ce mai mici, am ajunge în cele din urmă la celule, molecule sau atomi care nu mai pot fi împărțiți.
Cu toate acestea, folosind matematica, ne putem gândi la proprietățile pe care le-ar avea fractalii reali - iar acestea sunt foarte surprinzătoare ...
Dimensiuni fractale
În primul rând, să ne gândim la dimensiunea fractalilor. O linie are dimensiunea
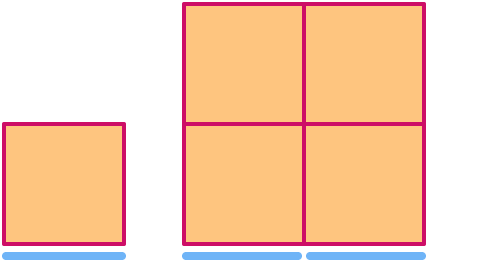
Un pătrat are dimensiunea
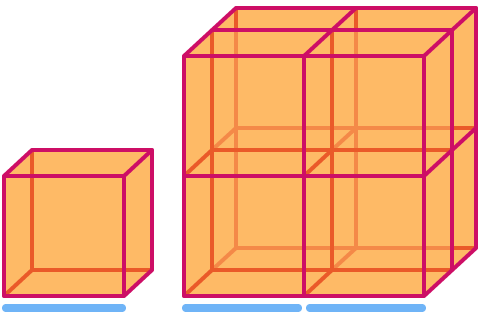
Un cub are dimensiunea
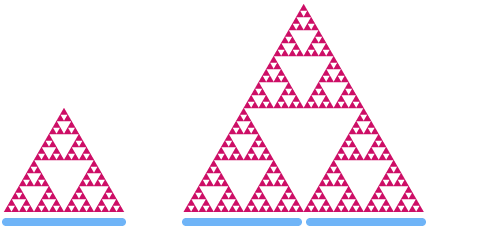
Acum să aruncăm o privire asupra triunghiului Sierpinski. Dacă îl scalăm cu un factor de 2, puteți vedea că „zona” crește cu un factor de
Să spunem că d este dimensiunea triunghiului Sierpinski. Folosind același model ca mai sus, obținem
Dar stai ... cum poate avea ceva o dimensiune care nu este un număr întreg? Pare imposibil, dar aceasta este doar una dintre proprietățile ciudate ale fractalilor. De fapt, acest lucru le dă numele fractalilor: au o dimensiune fracțională .
Cu fiecare iterație, eliminăm o parte din aria triunghiului Sierpinski. Dacă am putea face acest lucru de nenumărate ori, nu ar mai exista nicio zonă: de aceea triunghiul Sierpinski este ceva între o zonă bidimensională și o linie unidimensională.
În timp ce mulți fractali sunt similari cu sine , o definiție mai bună este aceea că fractalele sunt forme care au o dimensiune non-integrală .
Fulgul de zăpadă Koch
Există multe forme în natură care arată ca fractale. Am văzut deja unele plante la începutul acestui capitol. Alte exemple excelente sunt fulgii de zăpadă și cristalele de gheață:
Pentru a crea propriul nostru fulg de zăpadă fractală, trebuie să găsim încă o dată o procedură simplă pe care să o putem aplica din nou.
Ca și triunghiul Sierpinski, să începem cu un singur triunghi echilateral. Cu toate acestea, în loc să îndepărtăm triunghiuri mai mici la fiecare pas, adăugăm triunghiuri mai mici de-a lungul marginii. Lungimea laterală a fiecărui triunghi este
Forma rezultată se numește
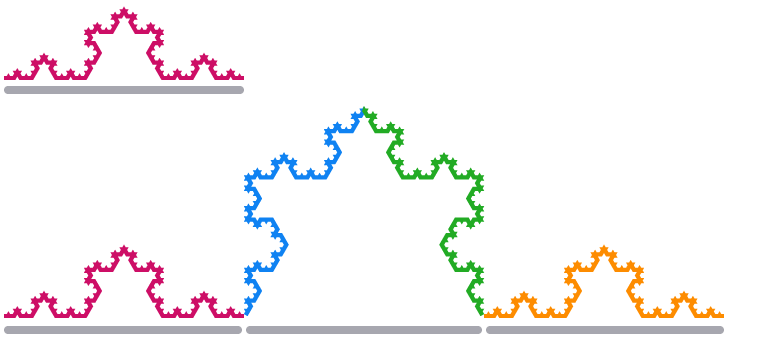
Când scalăm un segment de margine al fulgului de zăpadă Koch cu un factor de 3, lungimea acestuia se
Folosind aceeași relație între dimensiuni și factori de scară ca mai sus, obținem ecuația
Zonă
Crearea fulgilor de nea Koch este aproape ca o




După prima iterație, numărul de noi triunghiuri adăugate crește cu un factor de
Să spunem că
Folosind formula pentru suma
Perimetru
De asemenea, putem încerca să calculăm perimetrul fulgului de zăpadă Koch. După cum am văzut deja, lungimea perimetrului se modifică cu un factor de
Aceasta înseamnă că, încă o dată, avem o serie geometrică - dar, în acest caz,

Dacă acest lucru pare contraintuitiv, amintiți-vă doar că înmulțim perimetrul cu
Este aproape de neconceput că poți avea o formă cu o zonă finită și, de asemenea, o circumferință infinită - dar aceasta este doar una dintre numeroasele proprietăți neașteptate ale fractalilor.
Poți veni cu alte modalități de a-ți crea propriile fractale?
„Sufletul meu este în spirală pe fractale înghețate în jurul ...”
Biserica Menger
Fractalele nu trebuie să fie „plane”, ca multe dintre exemplele de mai sus. Unul dintre cei mai faimoși fractali care arată tridimensional este buretele Menger , numit după matematicianul
Începem cu un cub solid și găurim în mod repetat găuri mai mici și mai mici în laturile sale. Fiecare nouă iterație a găurilor are
A
Acum putem încerca să calculăm dimensiunea d a buretelului Menger la fel cum am făcut pentru fulgul de zăpadă Koch de mai sus. În acest caz obținem
Dacă vă imaginați tăind din ce în ce mai multe găuri, la infinit de multe ori, nu ar mai rămâne niciun volum real. De aceea, cubul este „nu tocmai” tridimensional!
Coasta fractală
Una dintre caracteristicile cheie ale tuturor fractalelor pe care le-am văzut până acum este că puteți „mări” pentru totdeauna și veți găsi întotdeauna modele noi. În jurul anului 1920, matematicianul britanic
Începeți cu forma de bază a țării și, pe măsură ce măriți, adăugați orificii de râu, golfuri și estuare, apoi stânci individuale, stânci, pietricele și așa mai departe:
Aceasta este o problemă semnificativă atunci când încercați să calculați lungimea graniței unei țări - cum decideți cât de mult să măriți și care sunt locurile și care sunt incluse?
Un mod în care am putea măsura lungimea liniei de coastă a Marii Britanii, de exemplu, este să luăm un conducător lung, să parcurgem toate plajele și apoi să adăugăm toate distanțele.
Dacă domnitorul este
Putem continua să mergem, cu stăpâni mai mici și mai mici, și de fiecare dată rezultatul nostru pentru lungimea coastei ar fi ceva mai lung. La fel ca și Fulgul de zăpadă de Koch înainte, se pare că coasta Marii Britanii este infinit de lungă! Acest lucru este adesea numit paradoxul litoralului .
Câteva decenii mai târziu, matematicianul
Litoralul Marii Britanii cu siguranță „arată” fractal, dar nu este similar cu sine , ca și alte fractale pe care le-am văzut anterior. Pentru a găsi dimensiunea acesteia, putem să o desenăm pe o grilă și să numărăm numărul de celule cu care se intersectează.
Inițial, există 88 de celule care se intersectează. Dacă am scala linia de coastă cu un factor de 2, există 197 de celule care se intersectează - mai mult de două ori mai multe!
Mărimea coastei a crescut cu un factor de
Dacă repetăm acest lucru cu grile mai mari, am constata că dimensiunea coastei britanice este de fapt aproximativ 1,21. Mandelbrot și-a dat seama că această dimensiune fractală este și o măsură a rugozității unei forme - un concept nou, pentru care a găsit aplicații importante în multe alte domenii ale matematicii și științei.
Mai multe fracturi în natură și tehnologie
În timp ce fractalii adevărați nu pot apărea niciodată în natură, există multe obiecte care arată aproape ca fractale. Am văzut deja plante, fulgi de zăpadă și linii de coastă și iată câteva alte exemple:
Lanțul montan din Asia centrală
Delta râului Ganges în India
Fulgere
Vasele de sânge din retină
Grand Canyon în SUA
nori
Toate aceste obiecte ar putea apărea complet aleatoare, dar, la fel ca fractalele, există un model de bază care determină modul în care sunt formate. Matematica ne poate ajuta să înțelegem mai bine formele, iar fractalii au aplicații în domenii precum medicina, biologia, geologia și meteorologia.
Teren fractal generat de computer
De asemenea, putem folosi fractali pentru a crea „copii” realiste, de exemplu, ca peisaje și texturi utilizate în jocuri video sau filme generate de computer. Apa, munții și norii din această imagine sunt realizate integral de un computer, cu ajutorul fractalilor!
Și chiar putem inversa acest proces pentru a comprima imagini digitale, pentru a reduce dimensiunea fișierului lor. Primii algoritmi au fost dezvoltați de Michael Barnsley și Alan Sloan în anii '80, iar altele noi sunt încă cercetate în prezent.