fractaliiSetul Mandelbrot

Toate fractalele pe care le-am văzut în capitolele anterioare au fost create folosind un proces de iterație : începeți cu un model specific, apoi îl repetați iar și iar.

Acest lucru este similar cu un alt concept în matematică pe care l-ați văzut anterior: cu secvențe recursive , începeți cu un număr specific, apoi aplicați aceeași formulă recursivă, din nou și din nou, pentru a obține următorul număr din secvență.

Să luăm formula recursivă xn=xn−12 ca exemplu, și descrieți termenii pe o linie numerică. Puteți modifica valoarea x0 :

Observați cum secvența rezultată se poate comporta foarte diferit, în funcție de valoarea de pornire x0 :

Până acum, nu am învățat nimic nou. Cu toate acestea, în urmă cu aproximativ un secol, matematicienii au început să exploreze ce se întâmplă cu aceste secvențe dacă utilizați numere complexe , mai degrabă decât doar linia de număr real. Descoperirile lor au fost unele dintre cele mai surprinzătoare și frumoase rezultate din toată matematica.

Julia Sets

Să folosim aceeași secvență ca înainte, xn=xn−12 , dar pe planul complex. Puteți muta poziția din x0 , pentru a vedea ce se întâmplă cu următorii termeni. Dacă secvența pare să convergă, hai să colorăm punctul corespunzător pe planul din albastru :

După cum puteți vedea, secvența converge cât timp x0 se află în cercul unității în afara pătratului unității deasupra x -axisului (cercul cu raza 1, centrat la origine).

Acum, să facem lucrurile un pic mai dificile. Mai degrabă decât să pătrundem numărul precedent, adăugăm și o constantă c de fiecare dată (care poate fi orice număr complex). Cu alte cuvinte, xn=xn−12+c . Crezi că tot vom obține un cerc de convergență? Ce alte forme credeți că am putea vedea? Continua

În această diagramă, puteți muta poziția x0 precum și valoarea de c :

Diferitele forme care se formează prin colorarea în numere se numesc seturi Julia . Au fost descoperite independent de doi matematicieni francezi, Gaston Julia și Pierre Fatou , în jurul anului 1918.

La acea vreme, nu existau computere care să ajute la vizualizarea cum arăta de fapt seturile Julia. Matematicieni precum Julia și Fatou au putut să argumenteze din punct de vedere matematic, dar au văzut vreodată doar schițe grosolane, desenate manual despre cum ar putea arăta.

Nu avem această problemă astăzi - imaginile de mai jos sunt diferite seturi Julia. Culorile diferite indică cât de rapid se diferențiază secvența din acel punct:

Continua

Setul Mandelbrot

Când creați diferitele seturi Julia, ați observat că există anumite valori ale c pentru care fiecare secvență se diverge și întregul plan complex rămâne alb. La câteva decenii după Julia și Fatou, o nouă generație de matematicieni a încercat să mapeze cum arătau aceste zone.

În exemplul precedent, am ales o valoare fixă pentru c , apoi a schimbat poziția din x0 pentru a colora avionul. Acum, să remediem valoarea de x0=0 și în schimb schimbați valoarea lui c .

Încă o dată, pictați pe planul complex pentru a dezvălui zona în care secvențele rămân delimitate. Ce forme așteptați să apară?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Acest fractal se numește setul Mandelbrot , iar atunci când este rotit cu 90°, pare aproape o persoană, cu cap, corp și două brațe. A fost definit și desenat pentru prima dată în 1978, într-o lucrare de cercetare de către matematicienii Robert Brooks și Peter Matelski:

Câțiva ani mai târziu, Benoit Mandelbrot a folosit computerele puternice de la IBM pentru a crea o vizualizare mult mai detaliată a fractalului, care a fost numit ulterior după el. Primele tipărituri arătau diferit de ceea ce se aștepta el - până când a realizat că tehnicienii care lucrează la imprimante curățau „neplăcerile” din jurul marginii sale, presupunând că acesta era cauzat de particule de praf sau erori ale imprimantei și nu o caracteristică definitorie a fractalilor. ! Continua

Ca toate fractalele, putem „mări” setul Mandelbrot pentru totdeauna, găsind noi tipare la fiecare scară. Aici puteți face zoom într-o parte a setului Mandelbrot care se numește vale Seahorse . Punctele negre sunt în interiorul setului Mandelbrot, unde secvența este delimitată. Punctele colorate se află în afara setului Mandelbrot, unde secvența se diverge, iar diferitele culori indică cât de rapid crește până la infinit:

Scale: ${pow(scale)}

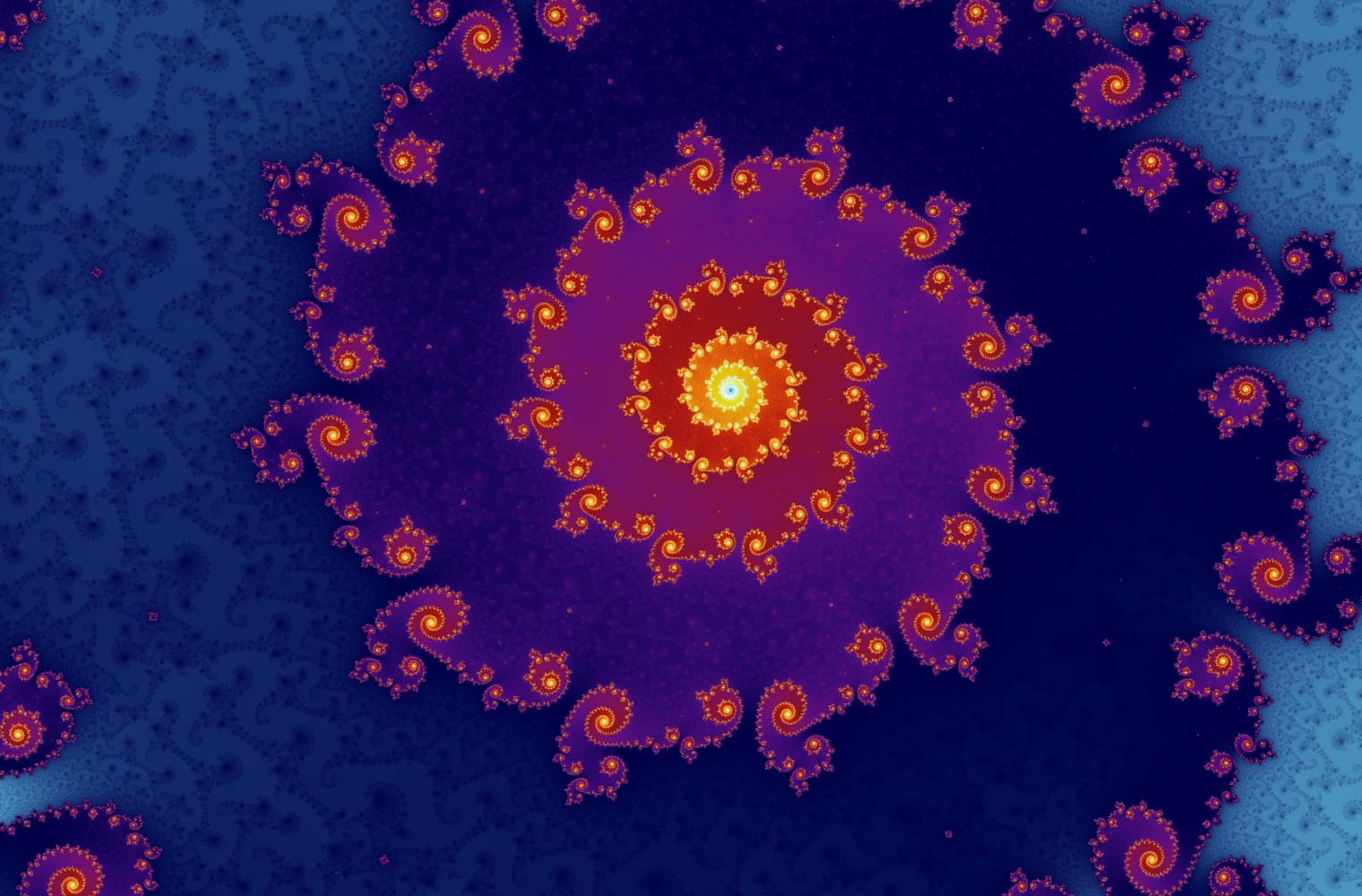
Acest glisor constă din 27 de imagini individuale, până la un nivel de zoom de peste 14 cvadrilioni sau 254 . În total, au avut nevoie de aproape 45 de minute să se redea pe un laptop modern. Setul Mandelbrot poate fi creat cu o singură ecuație simplă, xn=xn−12+c , cu toate acestea, este infinit de complex și uimitor de frumos.

Pe măsură ce mutați valoarea de c în jurul setului Mandelbrot, puteți observa o proprietate curioasă:

• Toate secvențele din corpul principal al setului Mandelbrot converg divergente ajunge pe o orbită într-un singur punct. * {.reveal(when="blank-0")} Secvențele din bulbul mare din vârf ajung pe o orbită converg divergente format din puncte. * {.reveal(when="blank-2")} Secvențele din acest bec mai mic au orbite de lungime .

Fiecare bec are o orbită de dimensiuni diferite, cu becuri mai mici având din ce în ce mai multe puncte pe orbitele lor. Mărimea acestor orbite sunt strâns legate de harta logistică , un concept important în teoria haosului .