Transformări și SimetrieGrupuri de Simetrie și Tapete
Unele forme au mai mult de o axă de simetrie - hai să aruncăm o privire la








Ai arătat deja anterior că un pătrat are
El are și simetrie rotațională cu
Și până la urmă, ne putem gândi la “nu face nimic” ca un alt tip special de simetrie – pentru că (evident) rezultatul este la fel ca înainte. Aceasta se numește uneori identitate.
Am găsit în total
Acum chiar putem începe să efectuăm operații aritmetice cu aceste simetrii. De exemplu, putem aduna două simetrii pentru a obține altele noi:






De fiecare dată când aduni două simetrii ale unui pătrat, obții una nouă. Iată aici un “calculator de simetrie” în care poți face încercări:
Joacă-te cu calculatorul de simetrie și încearcă să găsești modele. Poți completa aceste observații?
- Adunând două rotații se va obține mereu
(sau identitatea). - Adunând două reflexii se va obține mereu
(sau identitatea). - Adunând aceleași două simetrii în ordine opusă se va obține un rezultat
. - Adunând identiatea
.
Poate că ai observat deja că adunarea simetriilor este de fapt foarte asemănătoare cu adunarea numerelor întregi:
- Adunând două simetrii/numere întregi se va obține mereu o altă simetrie/un alt număr întreg:
+ = 12 + 7 = 19 - Adunarea simetriilor/numerelor întregi este
asociativă :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Orice simetrie/număr întreg are o/un invers(ă), o altă simetrie/un alt număr intreg care, atunci când e adunat, rezultă identitatea:
+ = 4 + –4 = 0
În matematică, orice colecție ce are aceste proprietăți se numește
În acest exemplu, am început cu cele opt simetrii ale pătratului. De fapt, orice formă geometrică are propriul ei grup de simetrie. Toate au diferite elemente care satisfac mereu cele trei reguli menționate mai sus.
Grupurile sunt prezente peste tot în matematică. Elementele pot fi numere sau simetrii, dar și polinoame, permutații, matrice, funcții … orice îndeplinește cele trei reguli. Ideea principală a teoriei grupurilor este că nu ne interesează elementele individuale, ci cum interacționează ele unele cu altele.
De exemplu, grupurile de simetrie a diferitelor molecule pot ajuta oamenii de știință să prezică și să explice proprietăție materialelor corespunzătoare.
Grupurile pot fi utilizate și pentru a analiza strategia câștigătoare în jocurile de masă. comportamentul virușilor în medicină, armonii diferite în muzică și multe alte concepte…
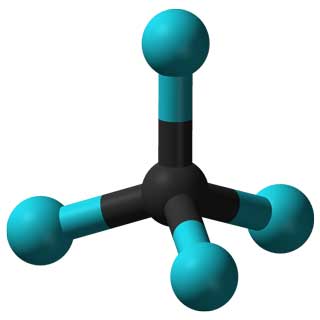
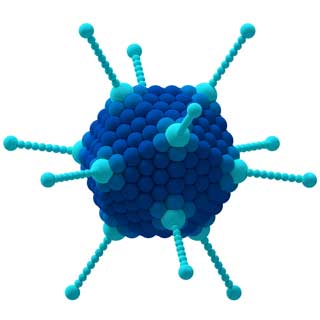
Proprietățile molecului CCl4 (stânga) și ale Adenovirusului (dreapta) sunt determinate de simetriile lor.
Grupuri de Tapet
În capitolele anterioare am văzut două tipuri diferite de simetrie ce corespund cu două transformări diferite: rotații si reflexii. Dar există și o simetrie pentru al treilea tip de transformare rigidă:


Fagure hexagonal


Plăci de faianță
Adițional simetriei reflexive, rotaționale și translative există chiar și un al patrulea tip:


Un șablon poate avea mai mult de un tip de simetrie. La fel ca la pătrate, putem afla
Aceste grupuri nu ne spun cum arată șablonul (ex: culorile și formele sale), ci doar cum se repetă. Multe modele diferite pot avea același grup de simetrie - atâta timp cât sunt aranjate și se repetă în același fel.


Aceste două șabloane au aceleași simetrii, chiar dacă arată foarte diferit. Dar simetriile nu au legătură cu culorile sau formele superficiale.


Și aceste două șabloane au aceleași simetrii – chiar dacă arată mult mai asemănator cu modelele corespunzătoare din stânga, decât una cu alta.
Se pare că, deși există o infinitate de șabloane posibile, toate au unul din cele 17 grupuri de simetrie diferite. Acestea se numesc grupuri de tapet.
Orice grup de tapet este definit de o combinație de translații, rotații, reflexii și reflexii cu alunecare. Poți vedea

Tip P1
Doar translații

Tip P2
Rotații de ordin 2, translații

Tip P3
Rotații de ordin 3 (120°), translații

Tip P4
Patru rotații de ordin 2 (180°), translații

Tip P6
Rotații de ordin 2, 3 și 6 (60°), translații

Tip PM
Axe paralele de reflexie, translații

Tip PMM
Reflexii perpendiculare, rotații de ordin 2, translații

Tip P4M
Rotații (ordin 2 + 4), reflexii, reflexii cu alunecare, translații

Tip P6M
Rotații (ord 2 + 6), reflexii, reflexii cu alunecare, translații

Tip P3M1
Rotații of order 3, reflexii, reflexii cu alunecare, translații

Tip P31M
Rotații of order 3, reflexii, reflexii cu alunecare, translații

Tip P4G
Rotații (ord 2 + 4), reflexii, reflexii cu alunecare, translații

Tip CMM
Reflexii perpendiculare, rotații de ordin 2, translații

Tip PMG
Reflexii, reflexii cu alunecare, rotații de ordin 2, translații

Tip PG
Reflexii cu alunecare paralele, translații

Tip CM
Reflections, glide reflections, translații

Tip PGG
reflexii cu alunecare perpendiculare, rotații de ordin 2, translații
Din păcate, nu se poate demonstra ușor de ce există 17 astfel de grupuri. Pentru a demonstra e nevoie de noțiuni matematice mult mai avansate…
În schimb, poți încerca să desenezi propriul tău șablon repetitiv pentru fiecare din cele 17 grupuri de tapet:
Examples of other students’ drawings



Grupurile de tapet se referă doar la șabloane plate, bidimensionale. Putem face ceva similar pentru șabloanele tridimensionale: acestea se numesc grupuri cristalografice și există 219 astfel de grupuri.
Pe lângă translații, reflexii, rotații și reflexii cu alunecare, aceste grupuri conțin simetrii plane de alunecare și axe elicoidale (te poți gândi la mișcarea de deșurubare a unui capac).
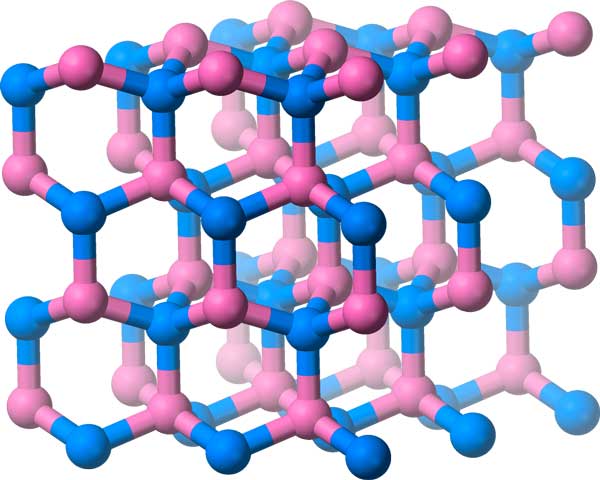
Nitrura cubică de bor are molecule aranjate într-o grilă de cristal, ce are un grup de simetrie tridimensional.