Poligoane și PoliedreMozaicări

Poligoanele apar peste tot în natură. Ele sunt utile în mod special atunci când vrem să pavăm o suprafață mare, pentru că poligoanele se pot potrivi împreună fără suprapuneri sau spații libere. Aceste tipuri de șabloane se numesc mozaicări.

Fagure de miere

Pielea șarpelui de lapte Sinaloan

Structura celulară a frunzelor

Coloane de bazalt de la Giant’s Causeway din Irlanda de Nord

Coajă de ananas

Carapacea unei țestoase

Oamenii au copiat multe din aceste șabloane naturale în artă, arhitectură și tehnologie – din Roma Antică până în prezent. Iată câteva exemple:

Model de pavaj

Seră din Proiectul Eden în Anglia

Mozaic de la Alhambra

Acoperiș la Muzeul Britanic din Londra

Pavilion cu mozaicări celulalre în Sydney

Studiul diviziunii regulate a planului cu reptile, M. C. Escher

Aici îți poți crea propriile mozaicări folosind poligoane regulate. Trage forme noi de pe bara alăturată pe pânza de lucru. Ce forme se mozaichează bine ? Există forme care nu se mozaichează deloc ? Încearcă să creezi modele interesante!

Exemple de mozaicări realizate de alți studenți

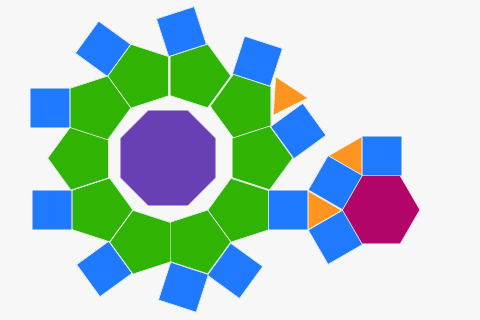
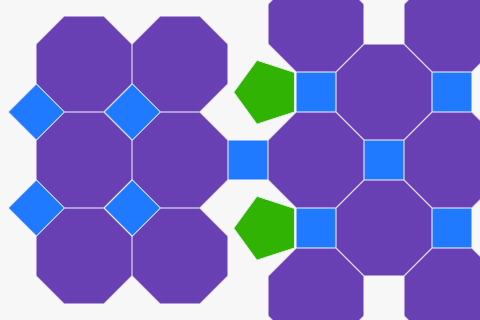
Mozaicări din poligoane regulate

Poate ai observat că unele poligoane regulate (precum ) se mozaichează foarte ușor, în timp ce altele (precum ) nu par să se mozaicheze deloc.

Aceasta are legătura cu măsura unghiurilor interne, despre care am învățat anterior cum se calculează. La fiecare vârf din mozaicare, se întâlnesc unghiurile interne ale multor poligoane diferite. Avem nevoie de toate aceste unghiuri pentru a însuma °, altfel vor exista goluri sau suprapuneri.

Triunghiurile pentru că 6 × 60° = 360°.

Squares pentru că 4 × 90° = 360°.

Pentagons pentru că multiplii lui 108° nu se pot însuma până la 360°.

Hexagoanele pentru că 3 × 120° = 360°.

În mod similar se poate verifica faptul că, asemeni pentagoanelor, orice poligon regulat cu 7 sau mai multe laturi nu se mozaichează. Aceasta înseamnă că singurele poligoane regulate care se mozaichează sunt triunghiurile, pătratele și hexagoanele!

Desigur că ai putea combina diferite tipuri de poligoane regulate într-o mozaicare, cu condiția ca unghiurile lor interne să însumeze 360°:

Pătrate și triunghiuri
90° + 90° + 60° + 60° + 60° = 360°

Hexagoane și triunghiuri
120° + 120° + 60° + 60° = 360°

Hexagoane și triunghiuri
120° + 60° + 60° + 60° + 60° = 360°

Hexagoane, pătrate și triunghiuri
120° + 90° + 90° + 60° = 360°

Octogoane și pătrate
135° + 135° + 90° = 360°

Dodecagoane (12-gaone) și triunghiuri
150° + 150° + 60° = 360°

Dodecagoane, hexagoane și pătrate
150° + 120° + 90° = 360°

Mozaicări din poligoane neregulate

Putem încerca să realizăm mozaicări și din poligoane neregulate – atâta timp cât suntem atenți când le rotim și le aranjăm.

Se pare că putem mozaica nu doar triunghiuri echilaterale, ci orice triunghi! Încearcă să muți vârfurile din această diagramă.

Într-un triunghi suma unghiurilor interne este °. Dacă folosim fiecare unghi la fiecare vârf în mozaicare, obținem 360°:

Și mai surprinzător, și orice patrulater se poate mozaica! Suma unghiurilor interne este de °, așadar dacă folosim fiecare unghi la fiecare vârf în mozaicare, vom obține 360°.

Pentagoanele sunt un pic mai complicate. Am văzut deja că pentagoanele regulate , dar cum rămâne cu cele neregulate?

Avem aici trei exemple diferite de mozaicări cu pentagoane. Ele nu sunt regulate, dar sunt poligoane cu 5 laturi perfect valide.

Până acum, matematicienii au găsit doar 15 tipuri diferite de mozaicări cu pentagoane (convexe) – cea mai recentă a fost descoperită în 2015. Nimeni nu știe dacă mai există și altele sau dacă cele 15 sunt singurele…

Mozaicări în Artă

Mozaicările sunt și un instrument, și inspirație pentru mulți artiști, arhitecți și designeri – cel mai faimos este artistul olandez M. C. Escher. Lucrările lui Escher conțin creaturi ciudate și mutante, șabloane și peisaje:

“Cer și Apăr I” (1938)

“Șopârlă” (1942)

“Șopârlă, Pește, Liliac” (1952)

“Fluture” (1948)

“Doi Pești” (1942)

“Scoici și Stele de Mare” (1941)

Aceste opere de artă arată adesea distractive și lipsite de efort, dar principiile matematice care stau la bază sunt aceleași ca mai înainte: unghiuri, rotații, translații și poligoane. Dacă calculele matematice nu sunt corecte, mozaicarea nu se va putea realiza!

“Metamorfoză II” by M. C. Escher (1940)

Plăcile Penrose

Toate mozaicările pe care le-am văzut până acum au ceva în comun: ele sunt periodice. Asta înseamnă că ele constau dintr-un model regulat care se repetă iar și iar. Ele se pot repeta la nesfârșit în toatele direcțiile și vor arăta la fel peste tot.

În anul 1970, matematicianul și fizicianul britanic Roger Penrose a descoperit mozaicări neperiodice – ele se tot continuă la infinit în toate direcțiile, dar nu arată niciodată exact la fel. Acestea se numesc Plăcile Penrose și ai nevoie de doar câteva tipuri diferite de poligoane pentru a crea una:

Mută glisorul pentru a dezvălui structura de bază a acestei mozaicări. Observă cum ai aceleași modele la diverse: pentagoanele mici și galbene, stelele albastre, romburile portocalii și ‘navele’ verzi apar la dimensiunea lor inițială, într-o măsură puțin mai mare și într-o măsură și mai mare. ăceastă auto-asemănare poate fi folosită pentru a demonstra că această placă Penrose este neperiodică.

Penrose a explorat mozaicările doar din amuzament, dar se pare că structura internă a unor materiale reale (precum aluminiul) au un șablon similar. Șablonul a fost utilizat chiar și pe hârtie igienică, deoarece producătorii au observat că un model neperiodic poate fi rulat fără nicio proeminență.

Schimbă limba

Conectați-vă la Mathigon

Acțiune

Resetați Progresul