Poligoane și PoliedreCorpurile lui Platon

La începutul acestui curs am definit poligoanele regulate ca fiind poligoane deosebit de “simetrice”, în care toate laturile și unghiurile sunt la fel. Putem face ceva asemănător și in cazul poliedrelor.

Într-un poligon regulat toate fețele sunt același tip de poligon regulat și în fiecare vârf se întâlnesc același număr de fețe. Poliedrele care au aceste două proprietăți se numesc corpuri platonice, numite după folosoful grec Platon.

Așadar cum arată corpurile platonice – și câte sunt? Pentru a construi o formă tridimensională avem nevoie de cel puțin fețe care să se întâlnească în fiecare vârf. Să începem sistematic cu cel mai mic poligon regulat: triunghiuri echilaterale:

Nici șapte sau mai multe triunghiuri care se întâlnesc în fiecare vârf nu determină poliedre noi: nu există suficient spațiu în jurul unui vârf pentru atât de multe triunghiuri.

Asta înseamnă că am găsit corpuri platonice formate din triunghiuri. Să trecem mai departe la urmatorul poligon regulat: pătratele.

În continuare, să încercăm cu pentagoane regulate:

Dacă în fiecare vârf se întâlnesc pentagoane, obținem un dodecaedru. Acesta are fețe. (“Dodeca” înseamnă “doisprezece” în limba greacă.)

Următoarele poligoane sunt hexagoanele:

Dacă în fiecare vârf se întâlnesc trei hexagoane, obținem o mozaicareun poliedruun hexaedru. Având în vedere că nu există spațiu pentru mai mult de trei, se pare că nu există corpuri platonice alcătuite din hexagoane.

La fel se întâmplă cu toate poligoanele regulate ce au mai mult de șase laturi. Ele nu se mozaichează și cu siguranța că nu obținem niciun poligon tridimensional.

Asta înseamnă că există doar corpuri platonice! Hai să ne uităm la toate la un loc:

De observat cum numărul de fețe si vârfuri se schimbărămâne la fel la cub și octaedru, precum și la dodecaedru și icosaedru, în timp ce numărul muchiilor rămâne mereu la fele diferit. Aceste perechi de corpuri Platonice se numesc corpuri duale.

Putem transforma un poliedru în varianta sa duală “înlocuind” fiecare față cu un vârf, și fiecare vârf cu o față. Aceste animație arată cum:

Tetraedrul este dual cu el însuși. Având în vedere că are același număr de fețe și vârfuri, înlocuirea lor nu ar aduce nicio schimbare.

Platon credea că toată materia din Univers este alcătuită din patru elemente: Aer, Pământ, Apă și Foc. El credea că fiecărui element îi corespunde un corp platonic, în timp ce al cincilea ar reprezenta universul ca un întreg. Astăzi știm că există peste 100 de elemente diferite ce sunt alcătuite din atomi sferici, nu din poliedre.

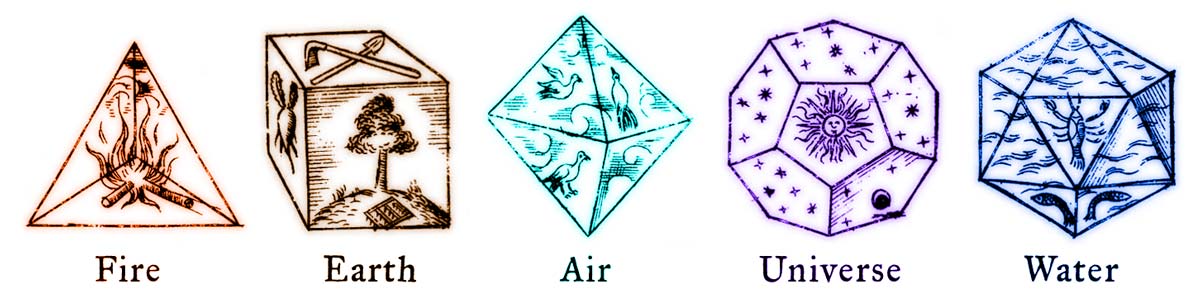
Imagini din cartea lui Johannes Kepler “Harmonices Mundi” (1619)

Corpurile lui Arhimede

Corpurile platonice sunt poliedre importante în mod deosebit, dar există nenumărate altele.

De exemplu, corpurile lui Arhimede tot trebuie să fie alcătuite din poligoane regulate, dar se pot folosi mai multe tipuri diferite. Numele lor e dat după un alt matematician grec, Arhimede din Siracuza, și există 13 astfel de corpuri geometrice:

Aplicații

Platon s-a înșelat crezând că toate elementele sunt alcătuite din corpuri platonice. Dar poliedrele regulate au multe proprietăți speciale care le fac să apară altundeva în natură - și putem copia aceste proprietăți în știință și inginerie.