Triunghiuri și TrigonometrieTeorema lui Pitagora

Am ajuns acum într-un punct important din geometrie – să putem formula și întelege una dintre cele mai faimoase teoreme din întreaga matematică: Teorema lui Pitagora. Această teoremă a fost numită după matematicianul din Grecia Antică Pitagora din Samos.

Teorema lui Pitagora Într-un triunghi dreptunghic, pătratul lungimii ipotenuzei (latura opusă unghiului drept) este egal cu suma pătratelor celorlalte două laturi. Altfel spus,

a2 + b2 = c2

Și reciproca este adevărată: dacă cele trei laturi ale unui triunghi satisfac relația a*{sup}2* + b*{sup}2* = c*{sup}2*, atunci triunghiul este .

Unghiurile drepte pot fi întâlnite peste tot și tocmai de aceea teorema lui Pitagora este atât de utilă.

Aici se poate vedea o scară cu lungimea de 6m ce stă sprijinită de un perete. Partea de jos a scării se află la 1m depărtare față de perete. Cât de departe se duce în sus pe perete?

De observat că există un triunghi dreptunghic format de scară, perete și sol. Folosind teorema lui Pitagora, obținem

h2+12	=62
⇒h2	=
⇒h	=35=5.92m

Pentru orice triunghi dreptunghic căruia îi știm două dintre laturi, putem folosi teorema lui Pitagora pentru a afla cea de-a treia latură.

Demonstrația Teoremei lui Pitagora

Teorema lui Pitagora era cunoscută vechilor babilonieni, mesopotamieni, indieni și chinezi, dar Pitagora a fost primul care a găsit o demonstrație matematică formală.

De fapt, teorema lui Pitagora poate fi demonstrată în mai multe moduri. Iată aici trei exemple diferite, fiecare utilizând o strategie diferită:

Rearanjare

Privește figura din dreapta. Pătratul are lungimea laturii a + b, și conține patru triunghiuri dreptunghice, precum și un pătrat mai mic cu aria .

Acum hai să rearanjăm triunghiurile în pătrat. Rezultatul conține încă cele patru triunghiuri dreptunghice, precum și două pătrate de dimensiunea .

Comparând aria suprafeței roșii înainte și după rearanjare, observăm că see that

a2+b2=c2.

Aceasta este demonstrația originală formulată de Pitagora.

c²

a²

b²

Algebra

Avem aici aceeași figură ca mai devreme, dar de data aceasta vom folosi algebra în loc de rearanjare pentru a demonstra teorema lui Pitagora.

Pătratul cel mare are lungimea laturii a+b și aria .

El constă din patru triunghiuri, fiecare având aria de , și un pătrat cu aria .

Dacă punem la un loc toate aceste informații, obținem

a+b2	=4×12ab+c2
a2+2ab+b2	=2ab+c2
a2+b2	=c2

Și, încă o dată, ajungem la teorema lui Pitagora.

Triunghiuri asemenea

Iată un alt triunghi dreptunghic. Dacă trasăm una din înălțimi, triunghiul se împarte în două triunghiuri mai mici. De asemenea, și ipotenuza c este împărțită în două părți mai mici pe care le vom numi x și y. Continuă

Hai să separăm cele două triunghiuri mai mici, astfel încât să fie mai clar cum sunt legate… Continuă

Ambele triunghiuri mai mici au un unghi comun cu triunghiul inițial. De asemenea, ele au și un unghi drept. Conform criteriului UU, toate cele trei triunghiuri sunt .

Acum putem folosi ecuațiile pe care le știm deja despre poligoane asemenea:

xa=ac

x=a2c

yb=bc

y=b2c

Continuă

Dar să ne amintim că c = x + y. Așadar

c=a2c+b2c

c2=a2+b2

Am demonstrat din nou teorema lui Pitagora!

Nu se cunosc multe detalii despre viața lui Pitagora și nu a fost găsită nicio lucrare de-a sa. El a fondat un cult religios numit Pitagorism care practica un soi de “venerare a numerelor”. Pitagoricienii credeau că toate numerele au propriile lor caracteristici și că urmează variate obiceiuri bizare.

Pitagoricienilor li se atribuie multe descoperiri matematice, inclusiv găsirea primului număr irațional, 2. Numerele iraționale nu pot fi exprimate ca fracții simple - concept care i-a tulburat profund pe pitagoricienii și pe care au încercat (fără succes) să-l ascundă!

“Pitagoricienii sărbătoresc răsăritul” de Fyodor Bronnikov

Calcularea Distanțelor

Una din cele mai importante aplicații ale teoremei lui Pitagora este calcularea distanțelor.

La dreapta se pot vedea duă puncte reprezentate într-un sistem de coordonate. Le-am putea măsura distanța folosind o rigla, dar nu ar fi suficient de precis. În schimb, să încercăm să folosim teorema lui Pitagora. Continuă

Putem număra cu ușurință distanța orizontală de-a lungul axei x, și distanța verticală de-a lungul axei y. Dacă desenăm acele două linii, obținem un triunghi dreptunghic. {.reveal(when="next-0")} Folosing teorema lui Pitagora,

d2	=${b.x-a.x}2+${b.y-a.y}2
d2	=${(b.x-a.x)(b.x-a.x) + (b.y-a.y)(b.y-a.y)}
d	=${(b.x-a.x)2+(a.y-b.y)2}=${round(distance(a,b),4)}

Această metodă funcționează pentru oricare două puncte:

Formula Distanței Fie două puncte de coordonate (x1,y1) și (x2,y2), atunci distanța dintre ele este

d2=x2−x12+y2−y12

d=x2−x12+y2−y12

Triplete pitagoreice

În timp ce mișcai vârfurile triunghiului din pasul anterior, poate că ai observat că în majoritatea cazurilor, lungimea ipotenuzei d era un . Totuși există câteva exemple de triunghiuri dreptunghice în care lungimile celor trei laturi sunt numere naturale.

Un exemplu binecunoscut este triunghiul 3-4-5. Întrucât 32+42=52, orice triunghi cu laturile de lungime 3, 4 și 5 este dreptunghic.

Vechii egipteni nu cunoșteau teorema lui Pitagora, dar știau despre triunghiul 3-4-5. Pentru construcția piramidelor ei au folosit sfori înnodate de lungimi 3, 4 și 5 pentru a măsura perfect unghiuri drepte.

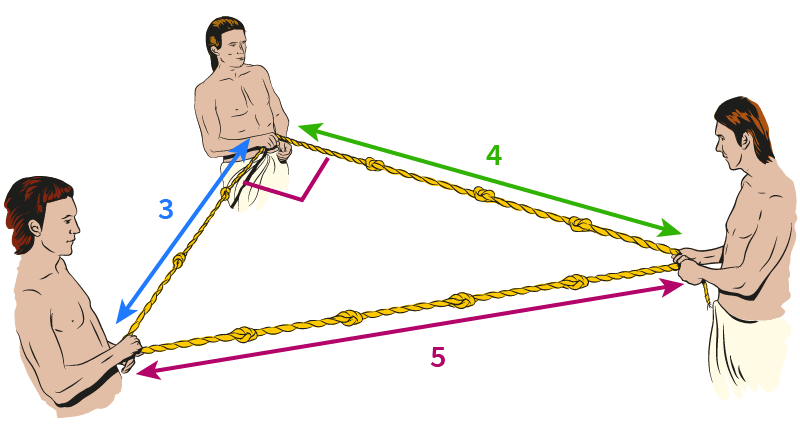
Trei astfel de numere întregi se numesc triplet pitagoreic. (3, 4, 5) este un exemplu de triplet pitagoreic. Dacă înmulțim fiecare număr cu 2, obținem un alt triplet pitagoreic: (6, 8, ).

Ne putem gândi la aceste triplete ca la niște puncte de grilă intr-un sistem de coordonate Pentru un triplet pitagoreic valid, distanța de la originea grilei va fi un număr natural. Poți găsi un alt triplet pitagoreic folosind sistemul de coordonate de mai jos?

${a.x}

${a.y}

${round(a.length,2)}

Observi un șablon în distribuția acestor puncte?

Schimbă limba

Conectați-vă la Mathigon

Acțiune

Resetați Progresul

Glosar